|
Aufgabe 1a: |
Auf den 11
Feldern eines Spieltisches liegen Geldbeträge so
verteilt, dass in jedem folgenden Feld ein
bestimmter Betrag mehr als im vorhergehenden liegt. |
Wie muss man 330 DM auf die Felder verteilen, damit
die Differenz der Einzelbeträge gleich groß wie
der Geldbetrag auf dem ersten Feld ist? |
|
|
4 P |
|
|
Aufgabe 1b: |
Welche Beträge
liegen in einer neuen Verteilung mit der Differenz
von 6,50 DM auf dem 1. und auf dem
11. Feld, wenn
auf dem letzten Feld 10 DM weniger als der
sechsfache Betrag des ersten Feldes liegen,
und
welche Summe liegt dann auf dem Spieltisch? |
|
|
4 P |
|
|
Aufgabe 1c: |
Auf wieviel
dieser Felder sind 420 DM zu verteilen, wenn die
Differenz 6 DM beträgt und auf dem ersten Feld
15
DM liegen? |
|
|
3 P |
|
|
Aufgabe 2a: |
| Sowohl das 1.
Glied als auch die Summe einer arithmetischen Reihe
beträgt 238, das 15. Glied ist Null. |
| Bestimme die
Differenz und die Anzahl der Glieder dieser Reihe. |
|
|
4 P |
|
|
Aufgabe 2b: |
| Sowohl das 1.
Glied als auch die Summe einer arithmetischen Reihe
beträgt 238, das 15. Glied ist Null. |
| Stelle eine in
n variable Formel zur Berechnung eines beliebigen
Gliedes dieser Reihe auf. |
|
|
4 P |
|
|
Aufgabe 2c: |
| Sowohl das 1.
Glied als auch die Summe einer arithmetischen Reihe
beträgt 238, das 15. Glied ist Null. |
| Berechne die
Summe der ersten 15 Glieder dieser Reihe. |
|
|
3 P |
|
|
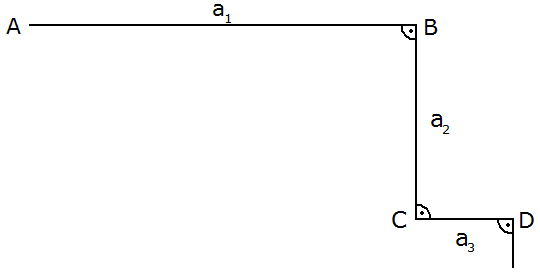
Aufgabe 3a: |
Die Strecken
 bilden den nebenstehenden Streckenzug. Die
Strecke
bilden den nebenstehenden Streckenzug. Die
Strecke
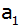 ist 8 cm lang, jede folgende Strecke ist die
Hälfte der vorhergehenden.
ist 8 cm lang, jede folgende Strecke ist die
Hälfte der vorhergehenden. |
| Wie lang ist die letzte Strecke des so
konstruierten Streckenzuges, wenn er
insgesamt 12 Knicke aufweist? |
|
 |
|
|
4 P |
|
|
Aufgabe 3b: |
Die Strecken
 bilden den nebenstehenden Streckenzug. Die
Strecke
bilden den nebenstehenden Streckenzug. Die
Strecke
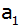 ist 8 cm lang, jede folgende Strecke ist die
Hälfte der vorhergehenden.
ist 8 cm lang, jede folgende Strecke ist die
Hälfte der vorhergehenden. |
Betrachtet man benachbarte Strecken des
Zuges als Seiten eines Rechtecks, dann
entsteht eine Rechteckfolge mit den
Flächeninhalten
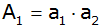 , ,
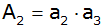 , ,
 . . |
| Berechne die Gesamtfläche der ersten 7
Rechtecke. |
|
 |
|
|
4 P |
|
|
Aufgabe 3c: |
Die Strecken
 bilden den nebenstehenden Streckenzug. Die
Strecke
bilden den nebenstehenden Streckenzug. Die
Strecke
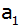 ist 8 cm lang, jede folgende Strecke ist die
Hälfte der vorhergehenden.
ist 8 cm lang, jede folgende Strecke ist die
Hälfte der vorhergehenden. |
Zeichne den Streckenzug bis
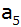 und verbinde seinen Endpunkt F mit A; zeige
dann durch Vergleich der Winkel
und verbinde seinen Endpunkt F mit A; zeige
dann durch Vergleich der Winkel
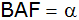 und
und
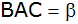 ,
dass die Strecke ,
dass die Strecke
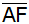 nicht durch Punkt C geht.
nicht durch Punkt C geht. |
|
 |
|
|
3 P |
|
|
Aufgabe 4a: |
In einem
regelmäßigen Sechseck mit der Seitenlänge
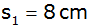 verbindet man die Mittelpunkte benachbarter
verbindet man die Mittelpunkte benachbarter
Seiten und erhält ein neues regelmäßiges Sechseck.
In diesem werden wieder die Mittelpunkte
benachbarter
Seiten zu einem Sechseck verbunden
usw. |
|
In welchem Verhältnis stehen die Umfänge zweier
aufeinanderfolgender Sechsecke? |
|
|
4 P |
|
|
Aufgabe 4b: |
In einem
regelmäßigen Sechseck mit der Seitenlänge
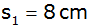 verbindet man die Mittelpunkte benachbarter
verbindet man die Mittelpunkte benachbarter
Seiten und erhält ein neues regelmäßiges Sechseck.
In diesem werden wieder die Mittelpunkte
benachbarter
Seiten zu einem Sechseck verbunden
usw. |
Zeige, dass die Flächen aufeinanderfolgender
Sechsecke den Verkleinerungsfaktor
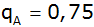 haben.
haben. |
|
|
4 P |
|
|
Aufgabe 4c: |
In einem
regelmäßigen Sechseck mit der Seitenlänge
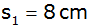 verbindet man die Mittelpunkte benachbarter
verbindet man die Mittelpunkte benachbarter
Seiten und erhält ein neues regelmäßiges Sechseck.
In diesem werden wieder die Mittelpunkte
benachbarter
Seiten zu einem Sechseck verbunden
usw. |
Welches Volumen hat ein Körper, der aus den ersten
10 Sechsecken besteht, wenn diese aus
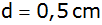
dicken Platten gestanzt und dann übereinander gelegt
worden sind? |
|
|
3 P |
|
|
Aufgabe 5a: |
In einem
rechtwinkligen Koordinatensystem sind drei Geraden
durch die Gleichungen
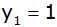 ; ;
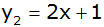 und
und
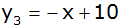 gegeben.
gegeben. |
Zeichne die Geraden in das Koordinatensystem mit der
Einheit 1 cm ein und weise durch Rechnung nach, dass
die
Geraden ein Dreieck mit den Eckpunkten
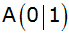 , ,
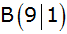 , ,
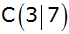 begrenzen.
begrenzen. |
|
|
4 P |
|
|
Aufgabe 5b: |
In einem
rechtwinkligen Koordinatensystem sind drei Geraden
durch die Gleichungen
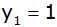 ; ;
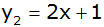 und
und
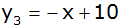 gegeben.
gegeben. |
Berechne die Seiten, die Winkel und die Höhe h über
der Grundseite
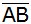 des Dreieckes ABC.
des Dreieckes ABC. |
|
|
4 P |
|
|
Aufgabe 5c: |
In einem
rechtwinkligen Koordinatensystem sind drei Geraden
durch die Gleichungen
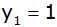 ; ;
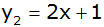 und
und
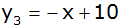 gegeben.
gegeben. |
|
Das Dreieck rotiert um die y-Achse. |
|
Wie groß ist das Volumen des entstehenden
Rotationskörpers? |
|
|
3 P |
|
|
Aufgabe 6a: |
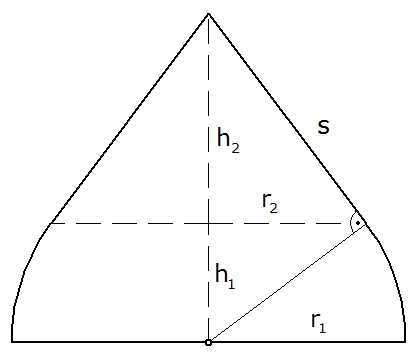
Das Dach eines Turmes hat die
nebenstehende Form einer Kugelschicht mit
einem kantenlos aufgesetzten Kegel (Maße:
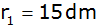 , ,
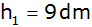 ). ). |
Zeichne einen genauen Achsenschnitt im
Maßstab 1 : 50, berechne die Größen
 , ,
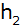 , ,
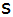 und die Verhältnisse
und die Verhältnisse
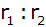 , ,
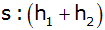 . . |
|
 |
|
|
4 P |
|
|
Aufgabe 6b: |
Das Dach eines Turmes hat die
nebenstehende Form einer Kugelschicht mit
einem kantenlos aufgesetzten Kegel (Maße:
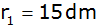 , ,
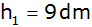 ). ). |
| Wie groß ist das Volumen des gesamten
Dachraumes? |
|
 |
|
|
4 P |
|
|
Aufgabe 6c: |
Das Dach eines Turmes hat die
nebenstehende Form einer Kugelschicht mit
einem kantenlos aufgesetzten Kegel (Maße:
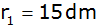 , ,
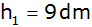 ). ). |
In welchem Verhältnis steht die
Mantelfläche
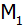 der Kugelschicht zur Mantelfläche
der Kugelschicht zur Mantelfläche
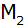 des Kegels?
des Kegels? |
|
 |
|
|
3 P |
|
|
Aufgabe 7a: |
Die Orte X, Y,
Z sind durch gradlinige Straßen miteinander
verbunden. Die Entfernungen betragen
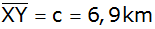 ; ;
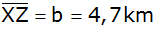 ; ;
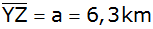 . . |
Fertige eine Zeichnung im Maßstab 1 : 100000 an und
berechne die Winkel (
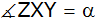 , ,
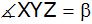 , ,
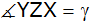 ),
unter denen sich die Straßen schneiden. ),
unter denen sich die Straßen schneiden. |
|
|
4 P |
|
|
Aufgabe 7b: |
Die Orte X, Y,
Z sind durch gradlinige Straßen miteinander
verbunden. Die Entfernungen betragen
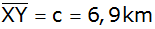 ; ;
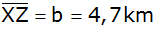 ; ;
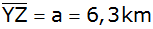 . . |
|
Berechne die Fläche, die von den drei Straßen
eingeschlossen wird. |
|
|
4 P |
|
|
Aufgabe 7c: |
Die Orte X, Y,
Z sind durch gradlinige Straßen miteinander
verbunden. Die Entfernungen betragen
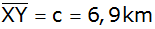 ; ;
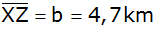 ; ;
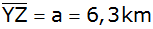 . . |
In
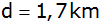 von X entfernt mündet in die Straße XY eine weitere
Straße, die parallel zur Straße XZ verläuft.
von X entfernt mündet in die Straße XY eine weitere
Straße, die parallel zur Straße XZ verläuft. |
|
Berechne die Trapezfläche, die dadurch im Dreieck
XYZ entsteht. |
|
|
3 P |
|
|
Aufgabe 8a: |
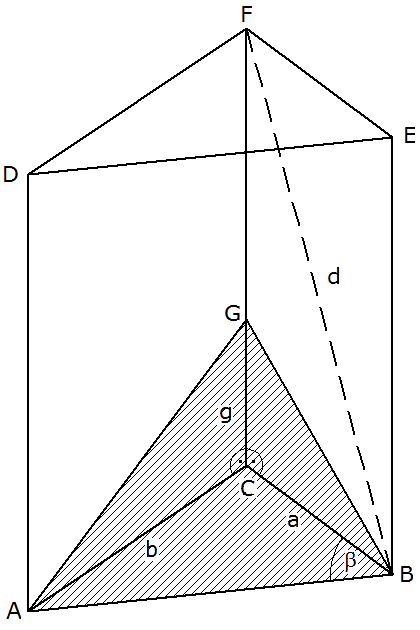 |
Das
obenstehende Prisma hat als Grundfläche ein Dreieck
mit den Seiten
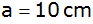 , ,
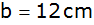 und dem
und dem
Winkel
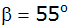 . . |
Wie hoch (h)
ist das Prisma und wie groß ist der Winkel
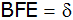 ,
wenn die Flächendiagonale ,
wenn die Flächendiagonale
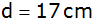
lang ist? |
|
|
4 P |
|
|
Aufgabe 8b: |
 |
Das
obenstehende Prisma hat als Grundfläche ein Dreieck
mit den Seiten
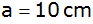 , ,
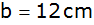 und dem
und dem
Winkel
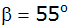 . . |
Diesem Prisma
ist das Dreieck ABG so einbeschrieben, daß
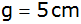 ist.
ist. |
Berechne die
Seiten (c, e, f) dieses Dreiecks und den Winkel
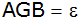 . . |
|
|
4 P |
|
|
Aufgabe 8c: |
 |
Das
obenstehende Prisma hat als Grundfläche ein Dreieck
mit den Seiten
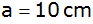 , ,
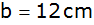 und dem
und dem
Winkel
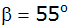 . . |
| Welches Volumen
hat das Prisma mit der Höhe g? |
|
|
3 P |
|