Home Geschichte Informatik Lernmaterial Linkliste Mathematik Smartphone ARS LB
1977 Übersicht
nach oben
Aufgabe 1a:
Subtrahiert man vom fünften Glied einer aus 15 Gliedern bestehenden arithmetischen Reihe das erste Glied, so erhält man 35.
Die Summe dieser beiden Glieder beträgt 50.
Berechne d, 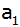, 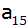und 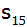dieser Reihe.
4 P
Aufgabe 1b:
Das erste Glied einer arithmetischen Reihe beträgt 1,5.
Das achte Glied dieser Reihe ist das 4fache des zweiten Gliedes dieser Reihe.
Die Summe aller Glieder dieser Reihe beträgt 82,5.
Wie groß sind d und n dieser Reihe?
4 P
Aufgabe 1c:
Eine arithmetische Reihe mit 16 Gliedern hat das Endglied 50.
Die Summe aller Glieder dieser Reihe beträgt 440.
Werden zu diesen 16 Gliedern 4 weitere Glieder addiert und danach alle Glieder um die Zahl k vermindert, so entsteht eine neue arithmetische Reihe 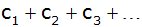, die ebenfalls die Summe 440 besitzt.
Bestimme k.
3 P
Aufgabe 2a:
Eine steigende geometrische Folge besitzt die beiden ersten Glieder 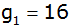und .
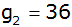Schalte zwischen je zwei Glieder der steigenden geometrischen Folge ein weiteres Glied so ein, dass wieder eine steigende geometrische Folge entsteht.
Wie groß sind das sechste Glied und die Summe der ersten sieben Glieder dieser neuen Folge?
4 P
Aufgabe 2b:
Eine steigende arithmetische und eine steigende geometrische Zahlenfolge haben beide das erste Glied 2 und stimmen auch im zweiten Glied überein.
Die Summe der ersten 3 Glieder der arithmetischen Reihe ist gleich dem 3. Glied der geometrischen Reihe.
Ermittle die ersten fünf Glieder beider Reihen.
4 P
Aufgabe 2c:
Das erste Glied einer steigenden geometrischen Folge ist 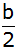und das dritte Glied .
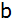Berechne 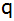dieser Folge.
Für welchen Wert von 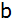gilt ?
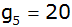Bestimme für den so ermittelten Wert von 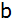die Anzahl aller Glieder dieser Folge, wenn das vorletzte
Glied 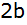ist.
3 P
Aufgabe 3a:
Von einem Dreieck sind die Seiten 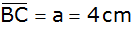und 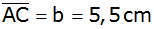sowie der Winkel
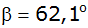
bekannt.
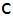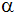Berechne die fehlende Seite , die fehlenden Winkel und 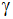sowie die Länge der Seitenhalbierenden
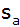
dieses Dreiecks ABC.
4 P
Aufgabe 3b:
Ein Dreieck ABC ist durch den Winkel 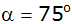, die Höhe 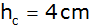und den Umkreisradius
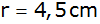
bestimmt.
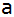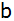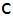Wie groß sind die Seiten , und , sowie die Winkel 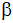und 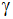des Dreiecks?
4 P
Aufgabe 3c:
Gegeben sind die beiden Kreise 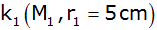und .
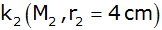Die Entfernung 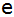der beiden Mittelpunkte dieser Kreise beträgt .
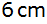Einer der beiden Schnittpunkte dieser Kreise sei .
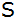Bestimme den Winkel 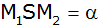und die Länge 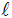der gemeinsamen Sehne beider Kreise.
3 P
Aufgabe 4a:
Ein in  rechtwinkliges Trapez ABCD hat folgende Maße:
Grundseite 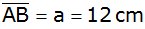, Diagonale 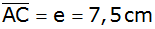, Winkel .
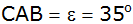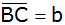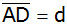Zeichne das Trapez maßstabgerecht, und berechne die Seiten und sowie
den Winkel 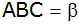dieses Trapezes.
4 P
Aufgabe 4b:
Von einem gleichschenkligen Trapez sind die Grunds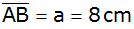eite , die Seite
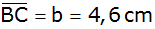
und die Diagonale 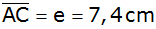bekannt.
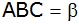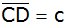Bestimme den Winkel , die Seite und den Flächeninhalt dieses Trapezes ABCD.
4 P
Aufgabe 4c:
Ein in A rechtwinkliges Trapez ABCD mit 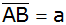und 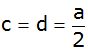rotiert um .
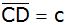Zeichne den Achsenschnitt dieses Rotationskörpers für .
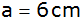Stelle eine Formel zur Berechnung des Rauminhaltes dieses Rotationskörpers in Abhängigkeit von a auf.
3 P
Aufgabe 5a:
In einem rechtwinkligen Koordinatensystem (Einheit 1 cm) ist ein Trapez durch die Punkte ,
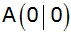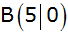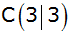, und 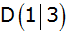gegeben.
Zeichne das Koordinatensystem und das Trapez.
1 P
Aufgabe 5b:
In einem rechtwinkligen Koordinatensystem (Einheit 1 cm) ist ein Trapez durch die Punkte ,
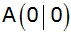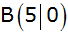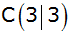, und 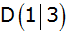gegeben.
Dieses Trapez rotiert um die x-Achse.
Berechne die Oberfläche 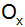dieses Rotationskörpers.
3 P
Aufgabe 5c:
In einem rechtwinkligen Koordinatensystem (Einheit 1 cm) ist ein Trapez durch die Punkte ,
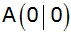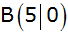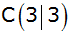, und 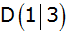gegeben.
Wie groß sind die Volumina 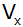und 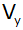, die durch Rotation dieses Trapezes um die x-Achse bzw. um
die y-Achse entstehen?
Weise nach, dass
 
gilt.
4 P
Aufgabe 5d:
In einem rechtwinkligen Koordinatensystem (Einheit 1 cm) ist ein Trapez durch die Punkte ,
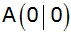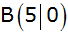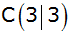, und 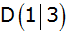gegeben.
Bei dem oben angegebenen Trapez schneiden sich die Verlängerungen der Seiten 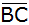und 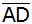über C bzw. über D hinaus in E.
Das Dreieck ABE rotiert um .
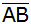Wie groß ist das Volumen 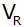dieses Rotationskörpers?
3 P
Aufgabe 6a:
Bei einer quadratischen Pyramide wurde die Höhe so gewählt, dass beim Achsenschnitt parallel zu einer
Grundkante ein gleichseitiges Dreieck mit der Seitenlänge 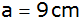entsteht.
Wie groß sind die Oberfläche, das Volumen und die Länge 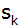einer Seitenkante dieser Pyramide?
3 P
Aufgabe 6b:
Bei einer quadratischen Pyramide wurde die Höhe so gewählt, dass beim Achsenschnitt parallel zu einer
Grundkante ein gleichseitiges Dreieck mit der Seitenlänge 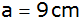entsteht.
Dieser Pyramide wird eine Kugel einbeschrieben.
Berechne das Volumen dieser Kugel.
3 P
Aufgabe 6c:
Bei einer quadratischen Pyramide wurde die Höhe so gewählt, dass beim Achsenschnitt parallel zu einer
Grundkante ein gleichseitiges Dreieck mit der Seitenlänge 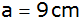entsteht.
Dieser Pyramide wird eine Kugel einbeschrieben.
Im Abstand des Kugeldurchmessers wird parallel zur Grundfläche ein Schnitt so geführt, dass diese Pyramide
in einen Pyramidenstumpf und die zugehörige Ergänzungspyramide geteilt wird.
Ermittle den Flächeninhalt der Schnittfläche und das Volumen des Pyramidenstumpfes.
3 P
Aufgabe 6d:
Einer Kugel mit dem Volumen 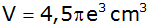soll eine quadratische Pyramide umbeschrieben werden,
deren Achsenschnitt parallel zu einer Grundkante ein gleichseitiges Dreieck darstellt.
Wie groß sind in Abhängigkeit von e der Radius r der Kugel und die Grundkante a der Pyramide?
Welchen Wert nimmt e an, wenn das Volumen der Pyramide 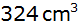beträgt?
3 P
Aufgabe 7a:
In einem rechtwinkligen Koordinatensystem (Einheit 1 cm) bilden die Punkte , ,
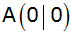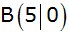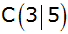
und 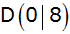die Eckpunkte eines Vierecks.
Wie groß sind die Seitenlängen a, b, c und d, die Innenwinkel 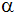, , 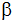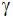und 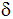sowie der Flächeninhalt dieses Vierecks?
4 P
Aufgabe 7b:
In einem rechtwinkligen Koordinatensystem (Einheit 1 cm) bilden die Punkte , ,
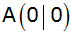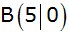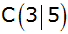
und 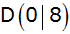die Eckpunkte eines Vierecks.
Dieses Viereck rotiert um die y-Achse.
Berechne das Volumen dieses Rotationskörpers.
Welchen Radius R hat ein Kegel von 8 cm Höhe, der dem Rotationskörper volumengleich ist?
4 P
Aufgabe 7c:
In einem rechtwinkligen Koordinatensystem (Einheit 1 cm) bilden die Punkte , ,
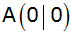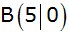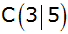
und 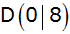die Eckpunkte eines Vierecks.
Der Punkt C wandert im ersten Quadranten auf einem Kreisbogen um A nach 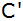, so dass die Geraden
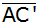
und 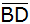senkrecht aufeinander stehen.
Wie groß ist die Entfernung ?
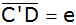3 P
Aufgabe 8a:
Die Dreiecke (1) und (2) erzeugen durch Rotation um die gegebenen Achsen bestimmte Rotationskörper.
 
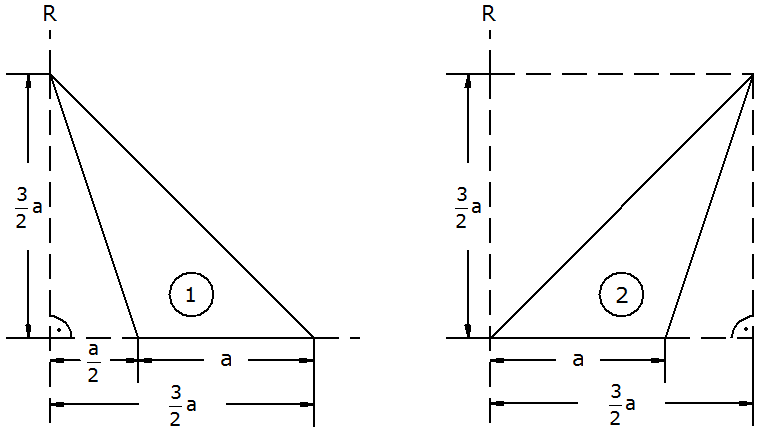Berechne für 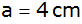die Oberfläche und das Volumen des Drehkörpers (2).
4 P
Aufgabe 8b:
Die Dreiecke (1) und (2) erzeugen durch Rotation um die gegebenen Achsen bestimmte Rotationskörper.
Leite für die Volumina der Drehkörper (1) und (2) Formeln in Abhängigkeit von der Variablen a ab und bestimme das Verhältnis, in welchem diese Volumina beider Körper zueinander stehen.
4 P
Aufgabe 8c:
Die Dreiecke (1) und (2) erzeugen durch Rotation um die gegebenen Achsen bestimmte Rotationskörper.
Ermittle die Oberfläche des Drehkörpers (1) in Abhängigkeit von der Variablen a. 
3 P
Aufgabe 9a:
1. Logarithmiere die Terme 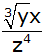und .
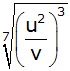2. Fasse die Terme
 
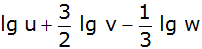  und
 
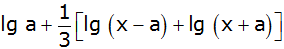  zu einem Logarithmus zusammen.
3. Logarithmiere den Term
 
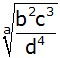  und berechne seinen Wert für a = 5, b = 2, c = 3 und d = 4.
4. Weise nach, dass die Beziehung
 
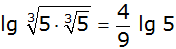  gilt.
4 P
Aufgabe 9b:
1. Zur graphischen Darstellung der Funktion 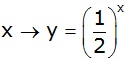sind zu den x-Werten
  - 3; - 2; - 1,5; - 1; - 0,5; 0; 0,5; 1; 1,5; 2; 3 
  die zugehörigen y-Werte zu bestimmen. 
2. Zeichne den Graphen im Intervall . 
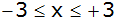3. Wie lautet die Gleichung der Umkehrfunktion von ?
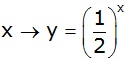4 P
Aufgabe 9c:
Gegeben ist die Funktion .
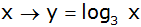Berechne die zu den x-Werten
 
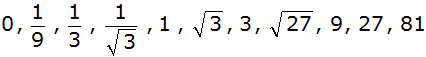zugehörigen y-Werte.
3 P
Aufgabe 10a:
1.  Beweise, dass
 
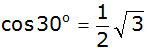  gilt.
2.  Bestimme aus der Zahlentafel
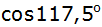    und .
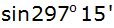3.  Gib alle Lösungen der Aussageformen 
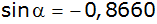  und
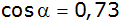  im Intervall 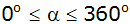an.
4 P
Aufgabe 10b:
Die Fläche eines Dreiecks läßt sich nach der Formel 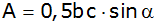bestimmen.
Tabelliere für b = 4cm und c = 6 cm im Intervall 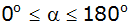die Abhängigkeit der Dreiecksfläche
vom Winkel 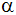in Schritten von .
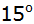Stelle diese Abhängigkeit der Dreiecksfläche von der Winkelgröße in einem rechtwinkligen Koordinaten-
system graphisch dar .
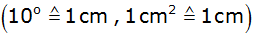4 P
Aufgabe 10c:
Weise durch Ableitung nach, dass der Kosinussatz auch im stumpfwinkligen Dreieck ABC 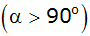gilt.
Wie groß ist die Seite 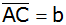im Dreieck ABC, wenn die Größen 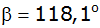, 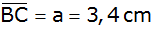und 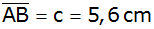gegeben sind?
3 P